ইলিয়ট ওয়েভ ও ফিবোনাচ্চি
ইলিয়ট ওয়েভ গানিতিক ভাবে গননায় ফিবোনাচ্চির সহয়তা প্রয়োজন।
ইলিওট ওয়েভ গণনা করতে এবং ভবিষ্যৎ প্রজেকশনের জন্য ফিবোনাচ্চি সহায়ক টুলস এবং ফিবোনাচ্চি ধারার সুত্রের সাথে এলিওট ওয়েভ গনণার সংখায় মিল থাকে। আপনি ওয়েভ কাউন্ট করতে ফিবোনাচ্চি লেভেল দেখতে সব কিছুতেই মিল পাবেন ।
ফ্রাক্টাল ও ফিবোনাচ্চি
মনে আছে আলোচনা করেছিলাম ফ্রাক্টাল? এখানে আমরা একটি ফ্রাক্টাল কে কিভাবে ফিবোনাচ্চি দিয়ে গণনা করতে পারি তা বুঝে যাবো।
ধরুন একটি গোলাপ ফুলের পাঁপড়ি ছিড়ছেন ।আচ্ছা ছিড়ার সময় নিশ্চয়ই গুণে দেখবেন না, কয়টা পাঁপড়ি থাকে। ১৩, ২১, ৩৪, ৫৫ কিংবা ৮৯ টা বা আরো বেশি কম । কিছুটা ব্যাতিক্রম ছাড়া প্রায় সব ফুলই এই নিয়ম মেনে চলে। অদ্ভুত মনে হচ্ছে? আসুন আরো চমক অপেক্ষা করছে। আপনি সায়েন্স কমার্স বা আর্টস যা নিয়ে পড়ুন না কেনো , অঙ্কে যথই দুর্বল হোন বা সুপার ডুপার হোন কোনো সমস্যা না সহজেই হিসাবটা করতে পারেন।
০, ১, ১, ২, ৩, ৫, ৮, ১৩, ২১, ৩৪, ৫৫, ৮৯, ১৪৪, ২৩৩, ৩৭৭…… এই যে সংখ্যাগুলো, এদেরকে বলা হয় ফিবোনাচ্চি সংখ্যা। অর্থাৎ, আগের সংখ্যার সাথে পরের সংখ্যাটা যোগ করলেই আরেকটি ফিবোনাচ্চি সংখ্যা পাওয়া যায়। কিছু ব্যতিক্রম ছাড়া সব ফুল এই নিয়ম মেনে চলে। শুধু ফুল নয়, প্রকৃতির অনেক জায়গায় এ সংখ্যা পাবেন। ফলেও ফিবোনাচ্চি সংখ্যা দেখা যায়। আনারসের “চোখ” গুণে দেখুন। এক সারিতে ৮ টা কিংবা ১৩ টা থাকে।
ফিবোনাচ্চি ইতিহাস
ফিবনাচ্চি সর্বপ্রথম আবিষ্কার করেন লিওনার্দো ফিবোনাচ্চি। তার জন্ম ইটালিতে। ফিবোনাচ্চির ধারা! মূলত তার নামানুসারেই হয়েছে, ১ ২০৩ খ্রিষ্টাব্দে খরগোশের প্রজননে তিনি সর্বপ্রথম এই ধারার অস্তিত্ব দেখতে পান। অর্থাৎ দুটি খরগোশ থেকে যদি প্রজনন হয়, আর একটা খরগোশও না মরে, তাহলে যদি ১০ মাস পর ৫৫ টা খরগোশ হয় ১১ মাস পর হবে ৮৯ টা, ১২ মাস পর হবে ১৪৪ টা।
বিখ্যাত Fibonacci ধারা/সিরিজ, এই সিরিজটি ভালভাবে লক্ষ্য করা দেখা যাবে প্রথম সংখ্যাটি বাদ দিলে প্রতিটি সংখ্যা আগের দুইটা সংখ্যার যোগফল, যেমন,
০ + ১ = ১, ১ + ১ = ২, ১ + ২ = ৩, ২ + ৩ = ৫, ৩ + ৫ = ৮, ৫ + ৮ = ১৩, ৮ + ১৩ = ২১, ১৩ + ২১ = ৩৪, ২১ + ৩৪ = ৫৫, ৩৪ + ৫৫ = ৮৯, ৫৫ + ৮৯ = ১৪৪, ১৪৪ + ২৩৩ = ৩৭৭… প্রভৃতি,
এবার নিচের ওয়েভের চিত্র টি দেখুন।।
ফিবোনাচ্চি নাম্বার এবং ইলিয়ট ওয়েভ গণনায় মিল।
১,১,২,৩,৫,৮,১৩,২১,৩৪,৫৫,৮৯,১৪৪ ফিবোনাচ্চি সংখ্যা।।
ইলিয়ট ওয়েভ হল মূলত ফ্রাক্টাল নিচের চিত্রে উদাহরন থেকে বোঝানোর চেষ্টা করছিঃ
আমরা সাপ্তাহিক চার্ট ওয়েভ ১ এবং ২ গণনা করলে ২টি (১+১)ওয়েভ দেখি। এই ওয়েভ আবার
প্রতিদিনের চার্টে আমরা আবার (১) (২) (৩) (৪) (৫) (a) (b) (C) ৮ টি( ৫+৩) ওয়েভ পায়।। একই ভাবে
ঘন্টার চার্টে আমরা এভাবে ১ ২ ৩ ৪ ৫ a b C করে 34 টি (২১ ইম্পালস + ১৩ কারেক্টিভ) ওয়েভ পায়।
এভাবে আমরা কম সময়ের ফ্রেমে গেলে পরবর্তী তে ৮৯ টি ইম্পালস ওয়েভ ও ৫৫টি কারেক্টিভ ওয়েভ পায়।
Fibonacci Golden Mean / Ratio :
Fibonacci অনুপাতগুলোর মধ্যে ০.৬১৮ এবং ১.৬১৮ হচ্ছে একটি আরেকটির বিপরীত অর্থাৎ, উভয়ের গুনফল হচ্ছে ১, এই ০.৬১৮ এবং ১.৬১৮ অনুপাত দুইটাকে Fibonacci Golden Mean / Ratio বলা হয় । প্রাকৃতিকভাবে এই অনুপাত দুইটা সবচেয়ে বেশী ব্যবহৃত হয়, অর্থাৎ,এই দুইটি অনুপাতে কোন বস্তুর হ্রাস এবং বৃদ্ধি বেশী ঘটে থাকে ।
আমরা আর একটু সহজ ভাবে দেখি – ১,১,২,৩,৫,৮,১৩,২১,৩৪,৫৫,৮৯,১৪৪্
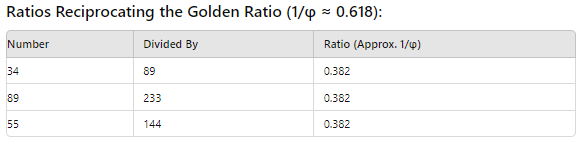
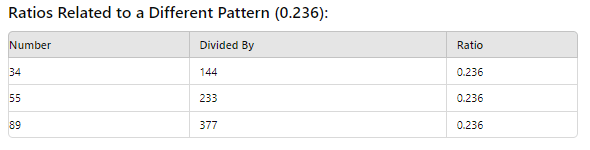
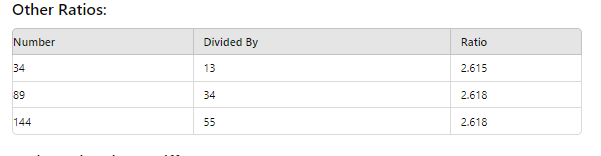
পাশাপাশি দুটি ফিবোনাচ্চি সংখ্যা গুলো কে আমরা পরের সংখ্যা দিয়ে ভাগ দিয়ে দেখি। আবার পরের সংখ্যা কে আগের সংখ্যা দিয়ে ভাগ দিয়ে দেখি। এভাবে আমরা আরো কিছু গোল্ডেন লেভেল পেতে পারি ।। যেমন ১৪৪ কে ৮৯ দ্বারা কিংবা ৫৫ কে ৩৪ দ্বারা ভাগ করলে ১.৬১ পাওয়া যাবে। আবার ৮৯ কে ১৪৪ দিয়ে ভাগ করলে ০.৬১৮ পাওয়া যায় একে বলে গোল্ডেন রেশিও।
মানবদেহের অভ্যন্তরীণ বিভিন্ন অঙ্গে এই গোল্ডেন নাম্বারের অস্তিত্ব পাওয়া যায়। একটা অঙ্গের দৈর্ঘ্যকে ১.৬১ দ্বারা গুণ করলে আরেকটা অঙ্গের দৈর্ঘ্যের সমান হয়।
নিচের টেবল গুলো থেকে বুঝার চেষ্টা করুন।সংখ্যা গুলো কিভাবে আগে পরে করে একটির সাথে আর একটি ভাগ দিয়ে গোল্ডেন নাম্বার গুলো পাওয়া যায়।


Add a Comment
You must be logged in to post a comment